The Pythagorean Theorem is a commonly used geometric theorem that states that the sum of the square of the legs of a right triangle is equal to the hypotenuse of the right triangle. Back in 490 BCE, a Greek mathematician named Pythagoras was credited with this theorem, however, studies have claimed that other mathematicians had founded this theorem before he did. Nowadays, the Pythagorean Theorem is being taught in middle and high schools, as young kids are learning how to apply this theorem into daily life.
Using the Pythagorean Theorem

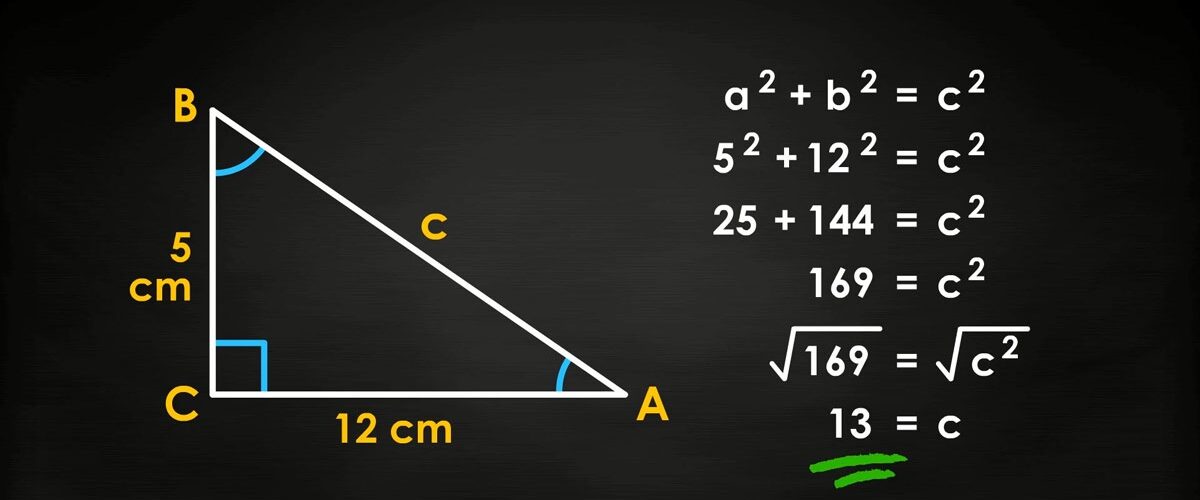
The formula for the Pythagorean Theorem is a2 + b2 = c2. The “a”, “b”, and “c” are all variables, meaning they can each be any number. The “c” value is the hypotenuse. A hypotenuse is the longest side of a triangle, located on the opposite side of the right angle. The “a” and “b” values are the legs of a triangle, which are both sides that are not the hypotenuse. This theorem can be a little tricky at first, but let’s look at some examples to understand how this theorem works.
Example 1:

If one length of a side of the triangle is 8, and another length of a side of the triangle is 6, then using the Pythagorean Theorem is needed to find the third side of the triangle (Side X). Because side x is the side that is opposite to the right angle, it is the “c” value. Therefore 6 and 8 are the leg values (Sides “A” and “B”). We must plug in 6 and 8 as A and B in the formula a2 + b2 = c2.
| Step 0) a2 + b2 = c2 | Pythagorean Theorem (initial formula) |
| Step 1) 62 + 82 = c2 | Substituted in values “6” and “8” for “A” and “B” because these are the leg lengths |
| Step 2) 36 + 64 = c2 | Squared 6 and 8. |
| Step 3) 100 = c2 | Combined like terms (36 + 64) |
| Step 4) √100 =√c^2. | Square rooted 100 and c2 to get rid of the square sign and to isolate the variable c |
| Step 5) 10 = c | Result of square root |
| Step 6) c = 10 | Reflexive Property. It is important to keep the variable on the left side of the equal sign as it is the proper notation |
Hopefully this makes sense to you and if it does not, then try to reread the steps or view Example 2. It takes practice to master the Pythagorean Theorem.
Example 2:

This one involves slightly bigger numbers, but we again have to find the “c” value as the length of the legs are given. To solve the equation, the formula a2 + b2 = c2 is needed. Because 12 and 16 are the leg values, 12 is the “A” Value and 16 is the “B” Value.
| Step 0) a2 + b2 = c2 | Pythagorean Theorem (initial formula) |
| Step 1) 122 + 162 = c2 | Substituted in values “12” and “16” for “A” and “B” because these are the leg lengths |
| Step 2) 144 + 256 = c2 | Squared 12 and 16. |
| Step 3) 400= c2 | Combine like terms (144 + 256) |
| Step 4) √400 =√c^2 | Square rooted 400 and c2 to get rid of the square sign and to isolate the variable c. |
| Step 5) 20 = c | Result of square root |
| Step 6) c = 20 | Reflexive Property. It is important to keep the variable on the left side of the equal sign as it is the proper notation |
This one was still a bit harder with the bigger numbers, and I can bet you that Example 3 will be even more challenging.
Example 3:

This one is a bit more tricky because the “C” value is already given. Therefore, finding the length of one of the base leg is needed, as the hypotenuse and one other base leg value are already given. The formula a2 + b2 = c2 is needed and the “a” value must be solved.
| Step 0) a2 + b2 = c2 | Pythagorean Theorem (initial formula) |
| Step 1) a2 + 242 = 262 | Substituted in values “24” and “26” for “B” and “C” because these are the leg lengths |
| Step 2) a2 + 576 = 676 | Squared 24 and 26 |
| Step 3) a2 = 100 | Subtracted 576 on both sides |
| Step 4) √a2 = √100 | Square rooted 100 and a2 |
| Step 5) a = 10 | Result of the square root |
When You Should NOT Use The Pythagorean Theorem
The Pythagorean Theorem can be used in many situations, although there could be times where the Pythagorean Theorem does not work. The theorem does not work with acute or obtuse triangles, or when one side length is given and you have to solve the other two. It only works for right-angled triangles, so you can use it to test whether a triangle has a right angle or not. Law of Sine/Cosine can be used as a replacement to the Pythagorean Theorem for acute and obtuse triangles.
Conclusion
The Pythagorean Theorem is a very commonly used and easy geometric proof to learn. The formula a2 + b2 = c2 will help you find a missing side length on a right triangle. All you need to do is plug in the lengths of two sides of a triangle in for “A”, “B”, “C”, in which “C” is the hypotenuse and “A” and “B” are the legs. There could be some situations in which the formula does not comprehend, such as triangles without a right angle.


Add comment