Introduction
If you know the lengths of all of the sides of any triangle, you can find the area of that triangle. You do not need to know any angle measures at all, just the side lengths. The formula to find the area of a triangle using only the side lengths is known as Heron’s Formula. I will first explain what Heron’s Formula is and how it works. Afterwards, we will go through a couple of practice problems using this formula.
Semiperimeter
If we have a triangle where the side lengths are $a,b,c,$ then the perimeter of the triangle is $a+b+c.$ We can state that the semiperimeter of the triangle is $\frac{a+b+c}{2}.$ We can denote the semiperimeter of a triangle as the variable $s.$ For example, if a triangle has side lengths $3, 4,$ and $5,$ the semiperimeter of the triangle is $6.$ If a triangle has side lengths $1,1,$ and $1$ the triangle has a semiperimeter of $3/2 = 1.5.$ The semiperimeter of a triangle is half the perimeter.
The Formula
This is Heron’s Formula:

$T$ represents the area of the triangle. Heron’s Formula states that if you define the semiperimeter of a triangle as $s,$ then the area of the triangle is the square root of the semiperimeter multiplied by the difference between the semiperimeter and all three sides. In other words, if $T$ is the area of the triangle, $s$ is the semiperimeter, and $a, b,$ and $c$ are the side lengths of the triangle, then $T = \sqrt{s \cdot (s-a) \cdot (s-b) \cdot (s-c)}.$ This formula may seem intimidating at first, but it is actually a very simple formula. We can now use this formula in some practice problems.
Examples
These are some problems that can be solved using Heron’s Formula. The first three problems are simply computational problems, but the last two require you to use tools besides Heron’s Formula to find the answer. First attempt these on your own and then read the solutions.
- 1. What is the area of a triangle with side lengths 2, 5, and 6?
- 2. If an equilateral triangle has side lengths of 14, then what is the area of the triangle?
- 3. If a triangle has side lengths of 3, 4, and 5, what is its area?
- 4. Isosceles triangle ABC has AB = AC = 7. If you draw the altitude from A to BC, the altitude intersects BC at point M. If BM = 4, find the area of triangle ABC.
- 5. Triangle ABC is similar to triangle XYZ. If AC/XZ = 2, and AB = 2, XZ = 9, and BC = 17, find the area of XYZ.
Solutions
Solution for Problem 1: The semiperimeter of the triangle is (2+5+6)/2 = 13/2. We know that 2 = 4/2, 5 = 10/2, and 6 = 12/2 so we can use Heron’s Formula. We can find the difference between s and all three sides as shown: s-2 = 9/2, s-5 = 3/2, and s-6 = 1/2. Therefore, Heron’s Formula states that the area of the triangle is the square root of (13/2 * 9/2 * 3/2 * 1/2). The expression in the parentheses is equal to 351/16. The square root of 351/16 is equal to (3 * sqrt{39})/4. So, the area of the triangle is equal to (3 * sqrt{39})/4 which is approximately 4.68.
Solution for Problem 2: Since the triangle is an equilateral triangle, all the side lengths are equal to 14. Therefore, its semiperimeter is (14+14+14)/2 = 21. The difference between the semiperimeter and each of the three sides is equal to 7. By Heron’s Formula, the area of the triangle is equal to sqrt{21 * 7 * 7 * 7} = 49 * sqrt{3} which is approximately 84.87.
Solution for Problem 3: The semiperimeter of this triangle is (3+4+5)/2 = 6. The differences between the semiperimeter and all three sides are 3, 2, and 1. Therefore the area of this triangle is sqrt{6 * 3 * 2 * 1} = sqrt{36} = 6. Therefore, the area of this triangle is 6. We also could have recognized that 3, 4, 5 is a Pythagorean Triple so the triangle is a right triangle. Since it is a right triangle, the area is the half the product of the two legs which is (3 * 4)/2 = 6. Because we got the same answer from two different ways, we can be confident that our answer is correct.
Solution for Problem 4: Since ABC is isosceles, the altitude from A to BC bisects BC. Therefore, M is the midpoint of BC. From this, we have BM = MC. We know that BM = 4, so BC = 8. Now, we know all three sides of triangle ABC so we can find the area. The semiperimeter is (7+7+8)/2 = 11. The differences between the semiperimeter and each of the sides are 4, 4, and 3. The area of triangle ABC is sqrt{11 * 4 * 4 * 3} = 4 * sqrt{33} which is approximately 22.98.
Solution for Problem 5: Since AC/XZ = 2, each of the sides of triangle ABC are 2 times the length of the corresponding sides in XYZ. XZ = 9 so AC = 18. In the problem, AB = 2 and BC = 17 were given to us. So, we know all the side lengths of triangle ABC. The semiperimeter of triangle ABC is (2+17+18)/2 = 37/2. The differences between the semiperimeter and each of the side lengths are 33/2, 3/2, and 1/2. By Heron’s Formula, the area of triangle ABC is sqrt{(37*33*3)/(16)} = (3 * sqrt{407})/4 which is approximately 15.13. Since AC/XZ = 2 and ABC and XZY are similar, the area of ABC is 4 times the area of XYZ. Therefore, the area of XYZ is the area of ABC divided by 4 which is approximately 3.78.
Conclusion
You have learned a very important formula that helps you find the area of any triangle if you know the lengths of all of the sides. I hope that you have learned a lot from this brief article. Thank you for reading.

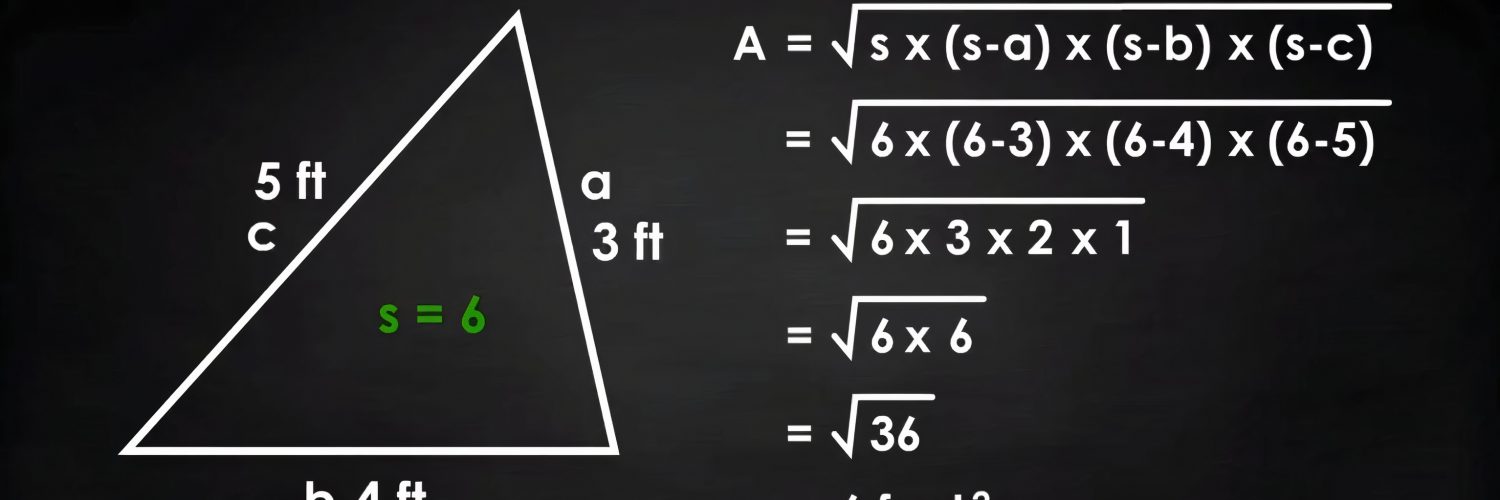
Let me know if you have any questions, I can answer all queries.
is it possible to do pythagoream theorem article??
Sure, I can make an article on the Pythagorean Theorem. If you tell me your email I can send the article to you when it is completed.