Logarithms are commonly known as the “opposite of exponents,” and are used to graph the inverse equation of exponents. While a standard exponential equation increases more and more along the x-axis, logarithmic equations increase less and less as x increases. When used in the real world, log equations are applied to many aspects of math and science, including pH in chemistry, the magnitude in physics, and survivability in biology.

Converting Logarithms
Essentially, a logarithm is a power that a base number is being raised to in an exponential equation. For example, in the equation 3² = 9, the base number, 3, is being raised to a power, which is 2. If we reverse this situation, we need to ask ourselves, “to what power is 3 raised in order to get 2?” We can break this thought process down into a couple of steps:
- The base number becomes the log base number. In 3², 3 is the base being raised. To do the opposite of raising, we must take create a logarithm. What was “three” is now “log base three,” or log₃ .
- The exponent number is moved to the other side of the equation.
- The end result (the number on the other side of the equal sign) is moved to the side with the log.
The end result should, in simpler terms, look like the two parts of the exponent have been separated, and the third number has been wedged in between.

Adding and Multiplying Logarithms
When two logarithmic expressions have the same log base, they can be freely added or multiplied. Addition and multiplication are interchangeable, and one can easily be converted to the other with the following equation:

Let’s take a look at the example log₂(4) + log₃(8). Because the log bases (2 and 3) are not the same, we cannot merge them into a multiplication equation. We can only leave them written out fully, also known as “expanded.” On the other hand, if we have log₂(4) + log₂(8), we can easily convert this to a multiplication expression by simply multiplying the numbers inside the exponents.

Subtracting and Dividing Logarithms
Just as addition can be converted to multiplication, subtraction in logarithmic equations can be condensed into division by putting the first term in parentheses under the second term in parentheses, then grouping them under the same log base. Again, this only works if the two expressions have the same log base, to begin with.

Let’s return to the example from above, but make it subtraction this time. In the expression log₂(4) – log₂(8), we can identify that the log base (2) is constant throughout. Next, all we need to do is combine them under than log base 2 umbrella, then divide 4 by 8. The end result comes out to be log₂( ⁴⁄₈ ).

Other Logarithm Rules
There are a couple of instances in which logarithmic equations either cannot be worked with or must be worked with in a specific way. These instances, as with many other math concepts, involve zero and ten.
- The zero rule: In a logarithm, log(0) is always undefined. This is because any number raised to another number will never be zero.
- The tens rule: Sometimes a log base is not indicated, such as in the expression log(5) rather than log₃(5). In these instances, the log base is always assumed to be 10. This is simply because scientists using logarithms found 10 to be easy to compute, and for their convenience, they wrote log(x) with the meaning of log₁₀(x).
Conclusion
Logarithms are an essential part of math, starting from algebra and branching into aspects of calculus. In short, they are the inverse of exponents and can be easily converted from addition and subtraction to multiplication and division, as well as the other way around.

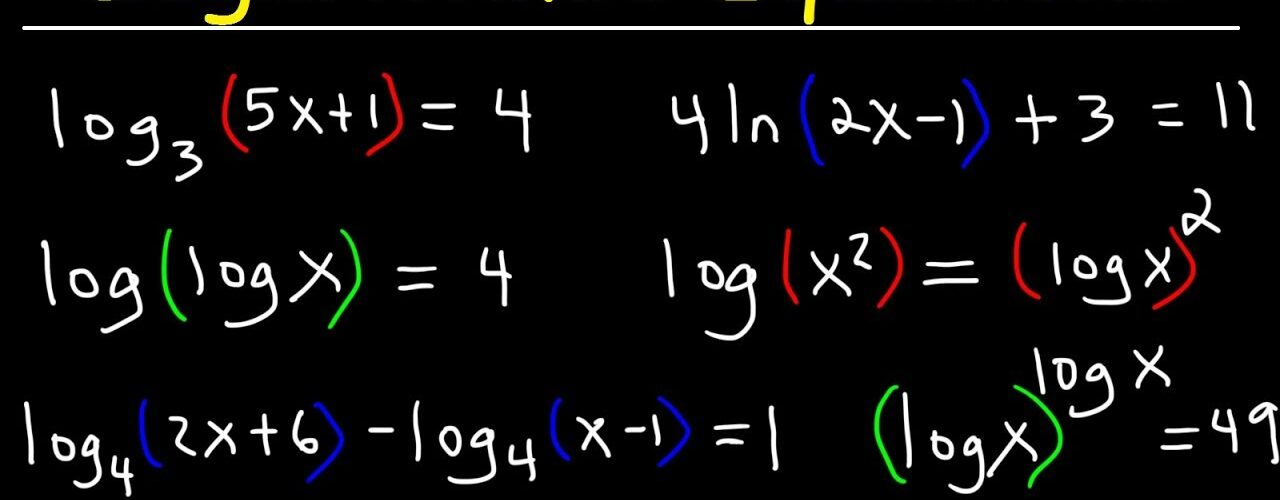
Add comment